| a. oplossen
van verminderde en overmatige intervallen
In de eerste paragraaf van dit hoofdstuk
is het onderscheid gemaakt tussen dissonante
en consonante intervallen.
Ieder dissonant interval vraagt als het ware een oplossing, en bovendien
kan meestal concreet worden gemaakt om welke oplossing het daarbij
gaat. Met andere woorden: bij dissonante intervallen ligt de voortzetting,
in de vorm van een bepaald consonant interval, op een bepaalde toonhoogte
(min of meer) vast.
Oplossen van verminderde
en overmatige intervallen is in feite het eenvoudigst - omdat bij
deze intervallen een eenvoudige regel kan worden geformuleerd over de oplossing:
| een verminderd interval lost krimpend op, een overmatig interval
spreidend. |
De bedoeling is daarbij dat beide tonen stapsgewijs
bewegen, de ene toon omhoog, de andere omlaag: |
| Toch is hiermee nog niet alles gezegd: we weten in feite nog niet hoeveel
de tonen van het verminderd of overmatig interval moeten bewegen. In principe
kan het bij 'stapsgewijze beweging' gaan om een grote of om een kleine
secunde. Zo kan de verminderde kwint b-f hierboven oplossen naar de grote
terts c-e, maar ook naar de kleine terts c-es.
Om het oplossen van verminderde en overmatige intervallen completer
te beschrijven moet daarom nog een tweede principe worden geformuleerd,
waarbij gebruik wordt gemaakt van het begrip 'leidtoon':
| bij een verminderd interval kan de onderste toon als leidtoon worden
beschouwd; bij een overmatig interval de bovenste. |
Zoals in 'toonsoorten
en toonladders' al gezegd: een leidtoon ligt altijd een kleine secunde
onder
de grondtoon. Of, vertaald naar het oplossen van verminderde en overmatige
intervallen: de toon die kan worden beschouwd als
leidtoon moet altijd een kleine secunde stijgen. De
andere toon daalt een grote of kleine secunde - waarbij er op gelet wordt
dat het oplossingsinterval consonant is. In het geval van de verminderde
kwint in het voorbeeld hierboven resulteert dit in twee mogelijke oplossingen:
zowel c-es als c-e is consonant. Bij de twee andere voorbeelden hierboven
(verminderd septime en overmatige secunde) is slechts een oplossing mogelijk.
Een oplossing naar a-es van het verminderd septime gis-f is niet mogelijk,
want a-es is een dissonant (verminderde kwint). En een oplossing naar f-b
van de overmatige secunde g-ais is evenmin mogelijk: f-b is een overmatige
kwart.
Nog een paar voorbeelden: |
| Een 'probleem apart' vormen de verminderde
kwart en de overmatige kwint : bij deze intervallen is het niet
mogelijk dat beide tonen bij het oplossen bewegen, omdat daardoor zou
worden 'opgelost' naar een dissonant interval: |
| In dit geval moet er daarom voor worden gekozen slechts een van beide
tonen te laten bewegen, en de andere toon te laten liggen. Het heeft daarbij
de voorkeur de leidtoon op te lossen (dus: te laten stijgen): |
| b.
omkering van verminderde en overmatige intervallen en hun oplossing
Verminderde en overmatige intervallen zijn elkaars
omkering. Zo levert de omkering van een verminderde kwint een overmatige
kwart op, omkering van een verminderde terts resulteert in een overmatige
sext enz. Als we de oplossingvan een verminderd
interval vergelijken met de oplossing van zijn omkering (een overmatig
interval dus) zien we dat ook de oplossingen
elkaars omkering vormen. Ofwel: de tonen van beide oplossingen zijn
dezelfde, alleen is een van d tonen een octaaf verplaatst: |
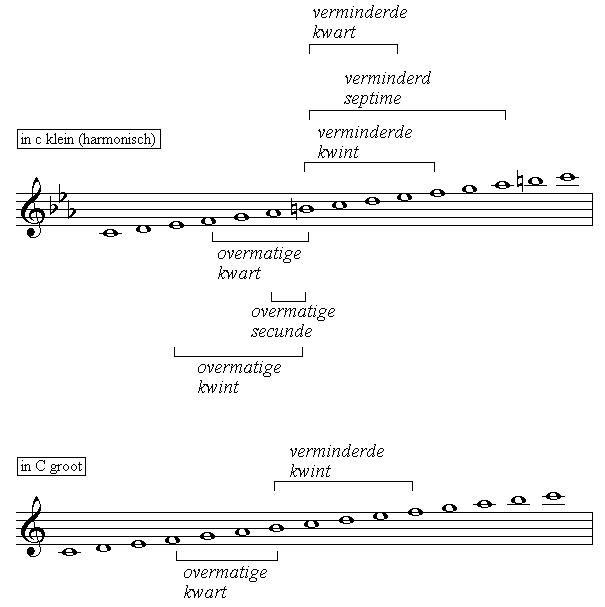
c. plaats in de toonsoort van verminderde en overmatige intervallen
Bij het oplossen van verminderde en overmatige intervallen wordt steeds
gebruik gemaakt van het begrip 'leidtoon'. Dit betekent ook dat een iets
andere benadering mogelijk is: we kunnen ons namelijk bij ieder verminderd
of overmatig interval ook (eerst) afvragen waar dit interval
in een toonsoort kan voorkomen.
Dat we een van beide tonen als leidtoon
beschouwen, betekent dat deze toon de zevende
toon van een toonladder is (en in mineur eigenlijk: de verhoogd
zevende
toon). We kunnen dan constateren dat
-
verminderde kwint en overmatige kwart voorkomen
tussen de tonen 7 en 4 van een majeur of (harmonische/melodische) mineurladder
-
verminderd septime en overmatige secunde voorkomen
tussen de tonen 7 en 6 van een (harmonische) mineurladder
-
verminderde kwart en overmatige kwint voorkomen
tussen de tonen 7 en 3 van een (harmonische/melodische) mineurladder:
|
| Iets lastiger is dit voor het interval-paar overmatige
sext/verminderde terts. Hierbij kunnen we er (vooralsnog) het beste
van uitgaan dat sprake is van een (kunstmatige) leidtoon voor de vijfde
toon van een mineur-toonsoort. Anders gezegd: de vierde toon van de toonsoort
wordt verhoogd, en verandert daardoor in een leidtoon voor de vijfde: |
Al het bovenstaande zou - nog iets completer en exacter
- ook
als volgt kunnen worden geformuleerd:
-
de intervalparen verminderde kwint/overmatige kwart, verminderd
septime/overmatige secunde, verminderde kwart/overmatige secunde en verminderde
terts/overmatige sext kunnen in principe slechts op één
manier worden opgelost, omdat het oplossingsinterval rein (volkomen
consonant) is. Verandering van het oplossingsinterval zou immers tot
gevolg hebben dat wordt 'opgelost' naar een dissonant: verandering van
de grootte van een rein interval maakt het verminderd of overmatig.
-
het intervalpaar verminderde kwint/overmatige kwart kan op
twee manieren worden opgelost, omdat het oplossingsinterval groot
of klein kan zijn (grote/kleine terts resp. grote/kleine sext). In
beide gevallen is het oplossingsinterval (onvolkomen) consonant.
-
bij het intervalpaar verminderde kwart/overmatige kwint kan
slechts een van beide tonen bewegen, omdat anders een dissonante
'oplossing' ontstaat. Oplossing van de leidtoon heeft de voorkeur, de andere
toon blijft liggen.
|
Een paar voorbeelden van oplossingen van verminderde en overmatige intervallen
vind je hier.
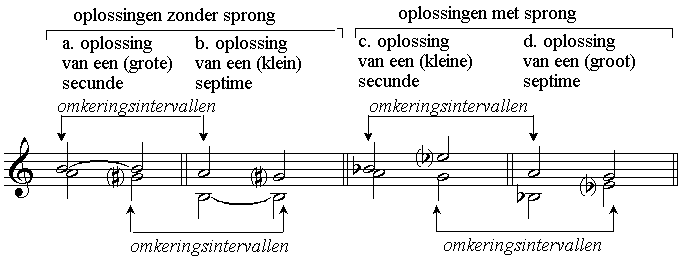
d. oplossing van secunde
en septime
Op het toelatings examen wordt hiernaar niet gevraagd. Maar voor de
volledigheid toch een enkele opmerking hierover.
Secundes en septimen lossen in principe altijd op naar een onvolkomen
consonant. Daarbij kun je er het beste van uigaan dat bij oplossing
van een secunde de onderste toon, en bij oplossing van een septime
de bovenste toon stapsgewijs daalt. Het maakt daarbij niet uit of
er sprake is van een grote of kleine secunde of septime: |
Uit het voorbeeld hierboven is op te maken dat bij de oplossing van
een grote secunde of een kleine septime een stap van een
grote
of een kleine secunde gemaakt kan worden: in de voorbeelden a. en b.
kan een b of een bes gebruikt worden. Bij de oplossing van een kleine
secunde
of een groot septime moet altijd een grote secunde-schrede gemaakt
worden (in de voorbeelden c. en d. is een bes in plaats van b uitgesloten).
In het voorbeeld wordt de suggestie gewekt dat er altijd een toon blijft
liggen. Maar dat hoeft niet: de bovenste toon van een secunde, of de onderste
van een septime kan naar een andere toon springen. Ik zou er daarbij vooralsnog
van uitgaan dat ook in dat geval de oplossing een onvolkomen consonant
vormt: |
| Dat bij een secunde de
onderste toon, en bij een septime juist de bovenste toon daalt is logisch
als je bedenkt dat secunde en septime elkaars omkeringsinterval
zijn: de oplossingen zijn dan ook elkaars
omkering: |
| e. de kwart als dissonant
interval
NOG MAKEN
|
|