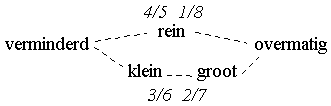| c. dissonante en consonante intervallen; intervalgrootte
Intervallen kunnen worden onderverdeeld in consonante
en
dissonante
intervallen. Het verschil tussen een consonant en een dissonant kan worden
begrepen als een soort 'spanningsverschil': dissonantie in de muziek creeert
spanning, consonantie ontspanning. Een tonaal muziekstuk zal niet snel
op
een dissonant eindigen - een dissonant vraagt als het ware om een voortzetting
in de vorm van een consonant, ofwel: een dissonant
verlangt naar een oplossing.
Bij de consonante intervallen wordt
bovendien een verschil gemaakt tussen volkomen en
onvolkomen consonant: een volkomen consonant is nog 'spanningslozer'
dan een onvolkomen.
Dit resulteert in de volgende
indeling:
-
consonante intervallen:
-
volkomen consonant: (rein) octaaf en
prime, (reine) kwint en kwart
-
onvolkomen consonant: (grote en kleine)
terts, (grote en kleine) sext
-
dissonante intervallen:
-
(grote en kleine) secunde, (groot en klein) septime
-
alle verminderde en overmatige intervallen
Intervallen kunnen verder worden onderscheiden naar hun grootte:
zo is de afstand van g naar b een terts, maar de afstand g-bes ook (in
beide gevallen gaat het om de afstand "3"). Het interval g-b is een grote
terts,
het interval g-bes een kleine terts.
We kunnen de terts nog kleiner maken: gis-bes - we spreken dan van een
verminderde
terts;
of nog groter: ges-b - dan spreken we van een overmatige
terts.
We kunnen dus tertsen van vier groottes onderscheiden.
Dat geldt ook voor sexten (omkeringsinterval van de terts), en ook voor
secundes en septimen. Zo is g-a een grote, g-as een kleine, en g-ais een
overmatige secunde (een verminderde secunde gis-as is een nogal 'theoretische'
constructie - deze tonen klinken immers gelijk).
Bij kwint en kwart, en octaaf en prime (de volkomen
consonanten) ligt de zaak een beetje anders: bij deze intervallen
is geen sprake van groot of klein. Zo wordt een kwint d-a
rein genoemd, als we deze kwint groter maken (d-ais bijvoorbeeld)
wordt hij overmatig; maken we hem kleiner,
dan wordt hij verminderd (d-as bijvoorbeeld).
De kwart d-g is rein, de kwart d-ges verminderd, en de kwart d-gis overmatig.
Een overzichtje om deze verschillen tussen enerzijds intervallen die
volkomen consonant kunnen zijn (4 en 5, en 1 en 8) en anderzijds 'de rest'
(3 en 6, en 2 en 7) te verduidelijken: |