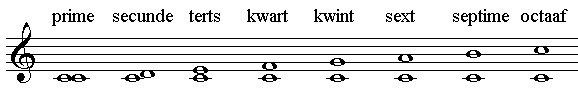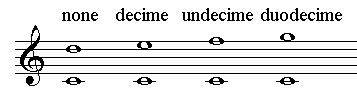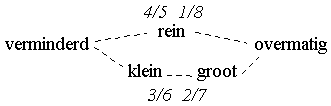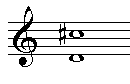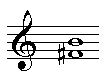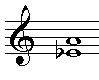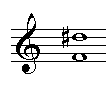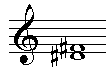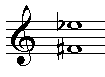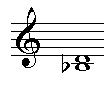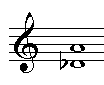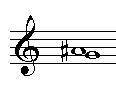De afstand tussen twee tonen wordt een interval genoemd. De intervallen hebben aan het latijn ontleende namen:

Zoals in bovenstaand voorbeeld te zien is, wordt een afstand van nul tonen aangeduid als prime, 'de eerste'. Dit doet op het eerste gezicht wat vreemd aan (de 'nulde' lijkt logischer); het hangt samen met het feit dat in de Oudheid het getal nul nog niet bestond.
Het octaaf is te beschouwen als bijna identiek aan de prime; we horen twee tonen in octaaf-afstand in feite als twee identieke tonen in een verschillend register, en niet als twee verschillende tonen. Dit wordt in ons toonsysteem tot uitdrukking gebracht doordat tonen op octaafafstand dezelfde naam hebben (C en c bijvoorbeeld).

Vanaf het octaaf herhalen de notennamen zich, zodat we intervallen groter dan het octaaf kunnen beschouwen als bijna-identieke broertjes van intervallen kleiner dan het octaaf (none lijkt op secunde, decime op terts enz.):

Met de bijzondere rol van het octaaf hangt ook samen dat intervallen kunnen worden beschouwd als elkaars omkering: twee intervallen die samen een octaaf vormen lijken op elkaar, en zijn elkaars omkeringsinterval. In feite wordt bij het omkeren van een interval een van beide tonen een octaaf naar boven of naar beneden verplaatst:

Door de eigenaardige manier van tellen van intervallen (zonder nul) vormen een interval en zijn omkeringsinterval samen het getal 9 (en niet 8):

Intervallen kunnen worden onderverdeeld in consonante en dissonante intervallen. Het verschil tussen een consonant en een dissonant kan worden begrepen als een soort 'spanningsverschil': dissonantie in de muziek creeert spanning, consonantie ontspanning. Een tonaal muziekstuk zal niet snel op een dissonant eindigen - een dissonant vraagt als het ware om een voortzetting in de vorm van een consonant, ofwel: een dissonant verlangt naar een oplossing.
Bij de consonante intervallen wordt bovendien een verschil gemaakt tussen volkomen en onvolkomen consonant: een volkomen consonant is nog 'spanningslozer' dan een onvolkomen.

Dit resulteert in de volgende indeling:

1. consonante intervallen:
• volkomen consonant: (rein) octaaf en prime, (reine) kwint en kwart
• onvolkomen consonant: (grote en kleine) terts, (grote en kleine) sext
2. dissonante intervallen:
• (grote en kleine) secunde, (groot en klein) septime
• alle verminderde en overmatige intervallen

Bij kwint en kwart, en octaaf en prime (de volkomen consonanten) ligt de zaak een beetje anders: bij deze intervallen is geen sprake van groot of klein. Zo wordt een kwint d-a rein genoemd, als we deze kwint groter maken (d-ais bijvoorbeeld) wordt hij overmatig; maken we hem kleiner, dan wordt hij verminderd (d-as bijvoorbeeld). De kwart d-g is rein, de kwart d-ges verminderd, en de kwart d-gis overmatig.

Een overzichtje om deze verschillen tussen enerzijds intervallen die volkomen consonant kunnen zijn (4 en 5, en 1 en 8) en anderzijds 'de rest' (3 en 6, en 2 en 7) te verduidelijken:

De vraag is nu: hoe te bepalen wanneer een interval groot, klein, overmatig of verminderd is. Daarvoor kan de volgende 'regel' worden geformuleerd:
 

Als we ons dus afvragen wat voor septimen c-bes en cis-bes zijn kunnen we constateren dat:

1. de bes niet voorkomt in C groot
2. de b wel voorkomt in C groot; c-b is dus een groot septime; c-bes is 'één stapje kleiner', en dus een klein septime.
3. cis-bes is nog een 'stapje kleiner'dan c-bes, en dus een verminderd septime

1. de fis voorkomt in D groot: d-fis is dus een grote terts (d-f zou een kleine terts zijn)
2. dis-f 'twee stapjes kleiner' is dan d-fis; dus is dis-f een verminderde terts

Een paar voorbeelden:

En een ander voorbeeld, waarbij alle intervallen op dezelfde toon zijn weergegeven; in het bovenste voorbeeld staan de grote en reine intervallen, in het onderste de kleine, verminderde en overmatige:
 

:

Hierboven is al gesproken over het feit dat intervallen elkaars omkering vormen. Als we bij het omkeren van intervallen ook naar de grootte van het interval kijken valt het volgende op (vergelijk met het muziekvoorbeeld hieronder):

• bij omkering van een rein interval ontstaat een (ander) rein interval; bijvoorbeeld: de reine kwart d-g wordt bij omkering de reine kwint g-d
• bij omkering van een groot interval ontstaat een (ander) klein interval; bijvoorbeeld: de grote terts d-fis wordt bij omkering de kleine sext fis-d. Het omgekeerde geldt (uiteraard) ook: omkering van een klein interval levert een groot interval op; zo wordt de kleine secunde d-es bij omkering het groot septime es-d
• bij omkering van een overmatig interval ontstaat een (ander) verminderd interval en vice versa; bijvoorbeeld: de overmatige kwart d-gis wordt bij omkering de verminderde kwint gis-d; de verminderde kwart b-es wordt bij omkering de overmatige kwint es-d

Gevraagd wordt het noteren van een bepaald interval op of onder een gegeven toon. Het is verstandig altijd als volgt te werken:

1. noteer de juiste intervalsoort(secunde, terts enz. op of onder de gegeven toon), oftewel: 'plaats het bolletje op de juiste plek in de notenbalk'. Dit is eigenlijk eenvoudig, want gewoon een kwestie van 'aftellen'
2. noteer de juiste intervalgrootte (klein, groot, verminderd, overmatig). Ga hierbij altijd uit van de 'regel voor de intervalgrootte': met andere woorden: ga uit van een groot of rein interval op of onder de gegeven toon.

Gevraagd wordt het benoemen van een bepaald interval. Het is verstandig op een vergelijkbare manier te werk te gaan als bij het noteren van intervallen

1. kijk naar de intervalsoort(secunde, terts enz.); dit is eigenlijk gewoon een kwestie van 'aftellen'
2. kijk naar de intervalgrootte (klein, groot, verminderd, overmatig). Ga hierbij altijd uit van de 'regel voor de intervalgrootte': met andere woorden: vraag je af hoe het gevraagde interval zich verhoudt tot een groot of rein interval op dezelfde toon..

tartget oplossen dissonante interallen algemeen
tartget oplossen verm ov