| c. consonante
en dissonante intervallen; versieringstonen; de kwart als consonant of
dissonant interval
Sommige intervallen wekken de indruk zeer stabiel
te zijn (er hoeft als het ware niets meer op te volgen); andere wekken
de indruk van spanning, activiteit, instabiliteit. De stabiele intervallen
worden consonant genoemd, de instabiele dissonant.
Bij consonante intervallen wordt bovendien een verschil gemaakt tussen
volkomen
en onvolkomen consonanten: volkomen consonanten
zijn nog 'spanningslozer' dan onvolkomen. Een overzicht:
| volkomen consonant |
reine prime, rein octaaf
reine kwint
reine kwart (maar niet altijd) |
| onvolkomen consonant |
grote en kleine terts
grote en kleine sext |
| dissonant |
alle secundes en septimen
alle overmatige en verminderde intervallen
soms: de reine kwart |
Consonante
intervallen zijn - anders gezegd - die intervallen die deel uitmaken van
een grote
of kleine drieklank, in grondligging of een omkering, al dan niet met
verdubbeling(en). Daarbij zijn de reine
intervallen het stabielst, gevolgd door de grote en kleine terts,
en daarna door de grote en kleine sext. De terts dus als iets stabieler
te beschouwen als zijn omkeringsinterval,
de sext. De reine kwint is stabieler dan zijn omkering, de reine kwart. De
kwart is bovendien een 'probleemgeval': hoewel volkomen consonant, wordt
de kwart toch vaak gebruikt en opgevat als een dissonant.
In onderstaand voorbeeld staan de consonante intervallen, van stabiel naar
'minder stabiel': |
| voorbeeld 73 |
| consonante intervallen |
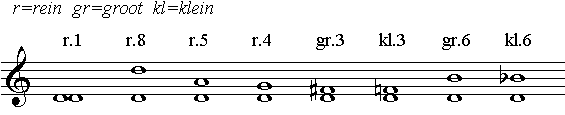 |
Prime en octaaf zijn in feite
volledig spanningloze intervallen; misschien dat om die reden in veel muziek
uit de Renaissance en van daarvoor prime en octaaf als
slot-interval van een stuk worden gebruikt.
Als volgende komt de kwint: in muziek die gebruik maakt van drieklanken
is de kwint van grote betekenis, omdat de bovenste toon van dit interval
er voor zorgt dat we de onderste als grondtoon van een akkoord horen.
Als we bijvoorbeeld de kwint d-a horen vatten we onmiddellijk de toon d
op als grondtoon, omdat d-a voorkomt in de grote of kleine drieklank op
d. Bovendien is de kwint tussen 1^ en 5^ (dus tussen tonica en dominant,
maar ook tussen grondtoon en kwint van de tonica-drieklank) van belang
bij het bepalen van de toonsoort. Als verdere 'informatie' ontbreekt (als
we dus alleen de tonen d en a te horen krijgen) zijn we geneigd aan te
nemen dat de toonsoort D groot of d klein is.
De grote drieklank is lange tijd beschouwd en behandeld als stabieler
dan de kleine. Dit betekent dus ook dat de grote terts als iets stabieler
te beschouwen is dan de kleine terts. Beide tertsen zijn 'actiever' dan
de kwint (actiever in die zin, dat een terts meer dan een kwint suggereert
dat voortzetting moet of kan volgen). De sext, omkeringen van de terts
is nog iets 'actiever', waarbij geen duidelijk verschil te maken
valt tussen grote en kleine sext.
In veel muziekstukken blijkt dat volkomen consonanten bijzonder geschikt
zijn voor belangrijke begin-
en eindpunten, vanwege het stabiele karakter van deze intervallen.
In muziekstukken met meer dan twee stemmen komen volkomen consonanten dan
vaak voor tussen de buitenstemmen op afsluitingen
en aan het begin. (dus: de afstanden 1, 5 of 8 tussen boven-en onderstem
- maar niet 4!) In de tussenliggende gedeeltes worden vaak meer onvolkomen
consonanten (en natuurlijk dissonanten) gebruikt, juist omdat deze eerder
in staat zijn het muzikaal verloop in beweging te zetten of te houden. Aan
het eind van stukken of gedeeltes daarvan komen
nog vaker volkomen consonanten voor dan aan het begin: kennelijk is
een 'stabiele afsluiting' van nog groter belang dan een 'stabiel begin'.
Anders dan de consonante intervallen komen dissonante intervallen niet
voor in de grote enkleine drieklank. Dissonanten tussen twee stemmen hebben
vaak te maken met 'melodische activiteit' in één of beide
stemmen. In het hoofdstuk 'tonaliteit
en muzikale structuur' stonden (naar aanleiding van de stabiele en
minder stabiele tonen in de toonsoort) de doorgang en de wisseltoon vermeld;
inderdaad treden dissonanten veelal op een dergelijke manier op: Als het
ware 'onderweg' van een consonant interval naar een volgend consonant interval,
en onderwijl spanning creërend. Consonante intervallen worden dan,
vaak stapsgewijs, door dissonanten omspeeld, versierd, met elkaar verbonden: |
Deze stapsgewijze beweging is een belangrijk
principe bij de omgang met dissonanten in tonale muziek (de zgn 'dissonantbehandeling');
stapsgewijze beweging zorgt voor een goede aansluiting van de dissonant
aan de consonante intervallen eromheen; het dissonante interval kan juist
dan goed als motor voor de melodische beweging fungeren. Omgekeerd bestaat
het gevaar dat dissonanten, die niet trapsgewijs bij consonanten aansluiten
als het ware doelloos lijken: het kan dan onduidelijk zijn waar de dissonant
'vandaan komt' en waar hij 'naar toe gaat'.
In het hoofdstuk 'tonaliteit
en muzikale structuur' hebben we gezien dat 2^, 4^, 6^ en 7^ als instabiele
tonen de neiging hebben naar 1^, 3^ of 5^ te bewegen. Dit heeft te maken
met dissonantie en consonantie: De 'actieve' tonen 2^, 4^, 6^ en 7^ vormen
immers een dissonant interval met één of meer tonen van de
tonica-drieklank; 1^, 3^ en 5^ daarentegen vormen onderling uitsluitend
consonante intervallen. Het meest primitieve gebruik van dissonanten zou
dan ook zijn: 1^, 3^ en 5^ als consonante basis gebruiken, en de andere
tonen uitsluitend als dissonante doorgangen: |
| Dit voorbeeld is uiteraard wel erg simplistisch, componisten gebruiken
natuurlijk ook andere - en subtielere - mogelijkheden. Eén belangrijke
mogelijkheid is: het ondersteunen (ook wel
genoemd: consonant maken) van de instabiele
tonen met behulp van een consonant interval; daarbij kunnen dan eventueel
1^, 3^ of 5^, dus de in de toonsoort stabiele tonen, op hun beurt als dissonant
optreden. Overigens verliezen 2^, 4^, 6^ en 7^ nooit helemaal hun instabiele
karakter, ook al worden ze ondersteund door een consonant interval. Dit
blijkt bijvoorbeeld als we onderstaande voorbeeld spelen, maar stoppen
op de derde tel van maat 1, of op de eerste tel van maat 2: deze punten
worden niet gehoord als mogelijke slot-momenten: |
| In de vroege Middeleeuwse meerstemmige muziek
vormden de volkomen consonanten de basis voor de muzikale compositie. Niet
alleen prime, octaaf en kwint, maar ook de kwart fungeerde als stabiel
interval. Dit is bijvoorbeeld het geval in het zgn. parallelorganum;
hierbij
werd een melodie begeleid in parallelle kwarten (onder de melodie), al
dan niet in combinatie met parallelle kwinten boven de melodie. Hieronder
twee voorbeelden van een streng organum
(uitsluitend
parallelle kwinten/kwarten, zie voorbeeld 77a en 77b) en van een
vrij
organum (aan het begin een prime;
vervolgens
tegenbeweging tot de kwart is bereikt; aan het eind weer tegenbeweging
tot de prime is bereikt - zie voorbeeld 77c). |
| voorbeeld 77 |
| a. streng organum in kwarten b. streng organum
in kwinten en kwarten c. vrij organum |
|
| In de loop der eeuwen gingen componisten er
toe over ook tertsen en sexten als consonante intervallen te gebruiken,
waardoor op den duur de drieklank de basis
voor de compositie werd. Dit betekende een fundamentele verandering van
de muzikale structuur, die onder andere tot gevolg had dat de rol
van de kwart veranderde. Aangezien de terts, als onderdeel van de
drieklank, ging optreden als stabiel interval, ontstonden situaties waarin
de kwart niet langer als stabiel, consonant interval kon worden beschouwd:
door het gebruik van de terts als consonant veranderde de kwart in een
'actief' interval, dat de neiging heeft naar de terts te gaan. Sinds de
late Middeleeuwen heeft de kwart daardoor in vele situaties het karakter
van een dissonant: |
| In tegenstelling tot situaties als in voorbeeld 78 (en in voorbeeld
80) blijft de kwart een consonant interval als hij bijvoorbeeld optreedt
in een gebroken akkoord, en we hem daardoor duidelijk horen als omkering
van de kwint: |
De kwart is dus 'anders' dan alle andere intervallen:
soms is hij consonant, soms dissonant. De kwart is consonant als uit de
context blijkt dat hij kan worden beschouwd als omkering van de kwint;
in alle andere gevallen is hij te beschouwen als dissonant. We kunnen stellen
dat de kwart in de praktijk dissonant is als hij
-
voorkomt in tweestemmige muziek, of
-
voorkomt tussen de onderstem en één van de hogere stemmen
in muziek met méér dan twee stemmen.
De functie van de verschillende intervallen zoals die voorkomen tussen
twee stemmen kan het beste worden gedemonstreerd aan de hand van tweestemmige
muziek uit de Renaissance: in deze muziek worden minder verschillende intervallen
gebruikt dan in muziek van later tijd. Dit
komt omdat muziek van voor ca.1600 modaal
is, en er nog bijna geen chromatiek voorkomt. Daardoor zijn verminderde
en overmatige intervallen betrekkelijk zelden: eigenlijk komen alleen de
verminderde kwint en overmatige kwart voor. Bovendien is deze muziek nog
min of meer zuiver lineair (horizontaal) gedacht: drieklanken
komen alleen voor als gevolg van de beweging in de stemmen, en zeker
niet
als melodisch element
Vooral omdat Renaissance-muziek primair vanuit horizontale lijnen is
gedacht maakt dat dissonanten tussen twee stemmen zich meestal volgens
een min of meer vast stramien gedragen: ze fungeren als doorgang
of
wisseltoon
op een licht maatdeel (en verbinden dan twee
consonante intervallen met elkaar), of als vertraging
(ook wel genoemd: voorhouding) op een zwaar
maatdeel. Dit laatste functioneert als volgt:
Uitgangspunt is bijvoorbeeld tweestemmigheid in parallelle
sexten. Natuurlijk kunnen daarbij beide tonen tegelijkertijd verschijnen
(zie voorbeeld 80a, links) - maar het kan ook gebeuren dat de tonen na
elkaar verschijnen (na elkaar intreden, zie
voorbeeld 80a, rechts.). Daardoor ontstaat op het zware maatdeel een dissonant
interval, dat vervolgens op het lichte maatdeel oplost naar een consonant
interval. In voorbeeld 80a gaat het om septimen die oplossen
naar een sext.
Vertragingen treden vrijwel altijd op een zwaar
maatdeel op; de dissonant wordt dus door het metrum benadrukt, krijgt
als het ware een accent. Dit in tegenstelling tot doorgang en wisseltoon,
die in het metrum juist niet worden benadrukt. De consonante intervallen
voor én na de vertraging staan dus op een lichter maatdeel (zie
voorbeeld 80b). Het consonante interval na de vertraging is de oplossing.
Het is altijd duidelijk welke van de
beide tonen de dissonant 'veroorzaakt' - in voorbeeld 80b is dit de
bovenste, in voorbeeld 80c de onderste toon. De vertraging wordt
vaak voorbereid (in Renaissance-muziek
gebeurt dit vrijwel altijd): een van de twee tonen van het consonante interval
voor
de
vertraging blijft liggen (of wordt herhaald) en vormt daardoor de vertraging
vormt (zie de voorbeelden 80c t/m f.). De liggendblijvende toon vormt dus
- op het moment dat hij nog consonant is - de voorbereiding
van de vertraging. Men kan dus bij een vertraging drie 'stadia' onderscheiden:
voorbereiding
(=consonant)
|
 |
vertraging
(=dissonant)
|
 |
oplossing
(=consonant)
|
In voorbeeld 80b functioneert dit dan als volgt: Voor de maatstreep
is de toon e consonant (=voorbereiding); na de maatstreep dissonant (=vertraging).
Op de tweede tel gaat de e naar d, waardoor weer een consonant interval
ontstaat (=oplossing). In de voorbeelden 80c en 80f heeft de onderstem
de vertraging; in 80d en 80e de bovenstem. In de voorbeelden 80 g, h en
i is te zien hoe een vertraging in een akkoord op kan treden (dus in muziek
met meer dan 2 stemmen); het principe is hetzelfde als in de tweestemmigheid;
de cijfers geven in deze laatste voorbeelden aan welk interval vertraging
en oplossing vormen met de grondtoon van het akkoord. |
| Een vertraging is eigenlijk niets anders dan dat één
toon, namelijk de oplossing 'iets te laat komt' (= vertraagd
wordt); het zou daarom niet logisch zijn als de oplossingstoon tegelijk
met de vertraging in een andere stem verschijnt: dit zou zoiets
als het verklappen van een geheim betekenen. Daarom ontbreekt
in de regel de toon waarnaar de vertraging oplost
in de klank waarin de vertraging verschijnt. Duidelijk zichtbaar
is dit in de voorbeelden 80g en 80 i.: In voorbeeld 80g ontbreekt
in de klank na de maatstreep de toon b (de terts; deze verschijnt in de
tweede helft van de maat als oplossing van de vertraging c); in voorbeeld
80i ontbreekt na de maatstreep de toon c (de terts; deze verschijnt in
de tweede helft van de maat als oplossing van de vertraging b). Uitzondering
zijn vertragingen die oplossen naar het octaaf: de toon waarnaar
de vertraging oplost is hierbij wél, namelijk als grondtoon,
tegelijk met de vertraging aanwezig (zie voorbeeld 80h: De toon d verschijnt
direct na de maatstreep, hoewel de vertraging e naar dezelfde toon oplost).
De reden voor deze uitzondering is eenvoudig te begrijpen: als we de grondtoon
van een klank zouden weglaten is deze nietmeerals zodanig herkenbaar, ,
en zou een andere toon als grondtoon worden gehoord; zo zou in voorbeeld
80h., als we na de maatstreep de toon d zouden weglaten, de toon f (in
de onderstem) de rol van grondtoon overnemen. |

|