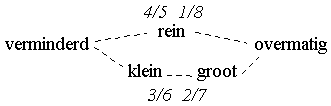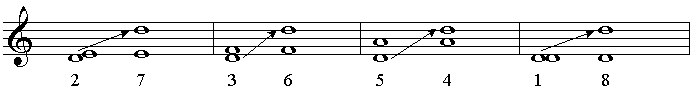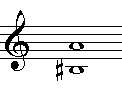a.
intervalsoort en -grootte; omkering van intervallen
In het eerste
hoofdstuk heb ik al een overzicht gegeven van de namen van de intervallen,
oftewel: van de verschillende intervalsoorten.
Intervallen
worden verder onderscheiden naar hun grootte.
Ik
ben er in de vorige hoofdstukken weliswaar enigszins van uitgegaan dat
de lezer al iets meer over
intervallen weet. Maar op dit punt is het zinvol e.e.a. op een rijtje
te zetten:
Er kunnen twee groepen intervallen
worden onderscheiden:
-
intervallen die in principe rein zijn: prime, octaaf,
kwint en kwart; als een rein interval een halve toon wordt verkleind
wordt het verminderd; als het een halve toon wordt vergroot wordt het overmatig
-
intervallen die in principe groot of klein zijn:
terts,sext, secunde en septime; als een groot interval een halve
toon wordt verkleind wordt het klein; als een klein interval een halve
toon wordt verkleind wordt het verminderd; als een groot interval een halve
toon wordt vergroot wordt het overmatig
Oftewel, in de vorm van een schema: |
| voorbeeld 59 |
| intervalgrootte |
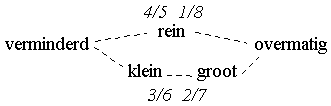 |
| Het 'vergroten' of 'verkleinen'
van een interval gebeurt chromatisch;
anders zou een ander
interval ontstaan: de terts cis-e kan worden vergroot tot cis-eis,
maar niet tot cis-f - dit laatste interval is geen terts, maar een kwart.
Voor beide groepen intervallen geldt:
een interval is groot of rein, als de
bovenste toon van het interval
voorkomt in de majeurladder die op de onderste
toon begint.
Een paar voorbeelden: |
| voorbeeld 60 |
| intervalgrootte |
a.verandering van een rein interval

b. verandering van een groot of klein interval
 |
Sommige van de intervallen in voorbeeld 60 zijn tamelijk theoretisch:
zo zal men niet snel een verminderd octaaf, een overmatige terts of een
verminderde sext tegenkomen. De volgende intervallen komen in de praktijk
voor:
| prime |
rein |
|
| secunde |
klein, groot, overmatig |
|
| terts |
verminderd, klein, groot |
|
| kwart |
verminderd, rein, overmatig |
(soms: dubbelovermatig) |
| kwint |
verminderd, rein, overmatig |
(soms: dubbelverminderd) |
| sext |
klein, groot, overmatig |
|
| septime |
klein, groot, verminderd |
|
| octaaf |
rein |
|
Intervallen opbouwen is tamelijk eenvoudig als de onderste toon grondtoon
van een gebruikelijke majeur-toonladder is; het is iets lastiger als de
onderste toon grondtoon van een majeur-ladder met veel voortekens is (tonen
als bis of fes), of als vanaf de bovenste toon moet worden gerekend.
Een paar 'rekenvoorbeelden': |
| 1a.vraag: benoem dit interval
Aangezien het lastig is zich de toonsoort Bis groot voor te stellen
negeren we het kruis in eerste instantie. b-a is een klein septime:
b-ais zou een groot septime zijn, aangezien ais in B-groot voorkomt; b-a
is een halve toon kleiner - dus een klein septime. Bis-a is dus een verminderd
septime,
want nog een halve toon kleiner dan het klein septime b-a |
voorbeeld 61
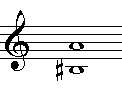 |
|
| 1b.vraag: benoem dit interval
De toon fis maakt geen deel uit van de majeurladder op as. Het interval
as-f komt wel voor in As groot, en is dus een grote sext. Door verhoging
van de F wordt het interval een halve toon groter dan deze grote sext:
as-fis is dus een overmatige sext. |
voorbeeld 62
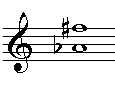 |
|
| 2a.vraag: noteer een verminderd septime onder bes.
Eerste stap: noteer de noot met de goede beginletter (een 'willekeurig'
septime onder bes), de toon c.
Volgende stap: we stellen vast dat c-bes een klein septime is:
c-b is immers en groot septime (de toon b komt voor in C groot). Een verminderd
septime is een halve toon kleiner dan een klein septime, dus: cis-bes.
(zie voorbeeld 63a.)
2b.vraag: Noteer een overmatige sext onder d.
Eerste stap: noteer de noot met de goede beginletter (een 'willekeurige'
sext onder d): de toon f.
Volgende stap: we stellen vast dat f-d een grote sext is (de
toon d komt voor in F groot). Een overmatige sext is een halve toon groter
dan een grote sext, dus: fes-d (zie voorbeeld 63b.) |
| voorbeeld 63 |
 |
Intervallen groter dan het octaaf worden samengestelde
intervallen genoemd, omdat ze
altijd te herleiden zijn tot een interval kleiner dan het octaaf (zie
voorbeeld 2 op pag.6). Zulke intervallen functioneren in de muziek eigenlijk
op dezelfde manier als de overeenkomstige intervallen binnen het octaaf.
Zo zouden we naar aanleiding van voorbeeld 14 (het thema van Mozart, Sonate
KV 331) kunnen stellen dat boven- en onderstem in parallelle tertsen bewegen.
Bij de analyse van stukken (en bij harmonie) maakt men eigenlijk vrijwel
uitsluitend gebruik van de none (9) en het decime (10); intervallen groter
dan een decime worden vaak weer kwart, kwint etc. genoemd (of: .kwart+octaaf,
kwint+octaaf enz.).
Uit het feit dat verschil wordt gemaakt tussen intervallen groter en
kleiner dan een octaaf blijkt dat het octaaf een bijzondere rol speelt:
eigenlijk is een octaaf geen 'echt' interval; als we twee tonen in octaaf-afstand
horen, nemen we in feite twee keer dezelfde toon waar, alleen in
een ander register. Daarom is dus bijvoorbeeld
een decime in feite een terts, waarbij de hoogste toon zich in een hoger
register bevindt.
Het octaaf is ook bepalend voor het feit dat intervallen elkaars omkering
zijn: intervallen kleiner dan een octaaf worden omgekeerd door de bovenste
toon een octaaf naar beneden, of de onderste toon een octaaf naar boven
te verplaatsen. Men kan de sext het omkeringsinterval
van de terts noemen, het septime van de secunde, enz. Voorbeeld 64 laat
zien welke intervallen elkaars omkering zijn: |
| voorbeeld 64 |
| omkering van intervallen |
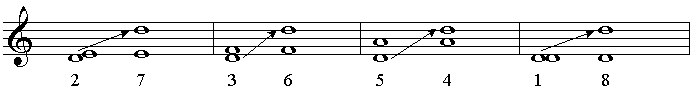 |
Het 'getal' van een interval
plus het 'getal' van zijn omkering is samen altijd 9:
|
|
|
|
| ______________________________+ |
|
|
De omkering van een rein interval is altijd
een (ander) rein interval. Voor de overige intervallen
geldt dat omkering ook de grootte van het interval
doet omkeren:
|
groot
|
<--->
|
klein
|
|
klein
|
<--->
|
groot
|
|
overmatig
|
<--->
|
verminderd
|
|
verminderd
|
<--->
|
overmatig
|
Een paar voorbeelden: |
| voorbeeld 65 |
| omkering van intervallen |
 |
| Aangezien omkering van een interval het gevolg is van octavering van
één van de twee tonen vormen een interval
en zijn omkering een verwant paar. Dit heeft natuurlijk weer met
de rol van het octaaf te maken: We horen bijvoorbeeld een grote terts en
een kleine sext als het ware als twee zijden van dezelfde medaille (zie
voorbeeld 65b). |
Bij omkering van samengestelde intervallen moet één van
de tonen twee octaven worden verplaatst. Het 'getal' van het interval
plus het 'getal' van zijn omkering is dan samen 16:
|
|
|
|
| ______________________________+ |
|
|
|
| voorbeeld 66 |
| omkering van samengestelde intervallen |
 |
| Men spreekt overigens vaak van omkering
als eigenlijk tegenbeweging
wordt bedoeld.
Dit is een veelgebruikt principe bij melodieën: alle stijgende intervallen
worden veranderd in dalende, en omgekeerd. Vaak is het hierbij voldoende
als alleen de soort, en niet ook nog de grootte van de intervallen
gelijk blijft: Een stijgende grote terts kan dus dan bijvoorbeeld een dalende
kleine terts worden enz. (zie voorbeeld 67). Soms blijft ook de grootte
van de intervallen onveranderd. Dan is sprake van een 'echte'
omkering.
Deze wordt ook wel spiegeling
genoemd (zie voorbeeld 68). |
| voorbeeld 67 |
| J.S.Bach: das wohltemperierte Klavier, band I, fuga
in fis kl.t. |
|

|